ALEM
Algoritmo de maximização de expectativa
O que é ?
É um método interativo baseado em uma maximização para estimar os parâmentros da distribuições a partir dos dados da amostra. Os dados podem ser variáveis latentes, ou seja, não observadas de forma quantitativa inicialmente, nesta ferramentas pode utilizar o banco de dados com dados faltantes, pois em uma das etapas ocorre a imputação de dados para estimar o modelo.
A iteração EM alterna entre executar uma etapa de expectativa (E) e uma de maximização (M). A etapa de expectativa cria uma função para a expectativa da verossimilhança logarítmica usando a estimativa atual para os parâmetros. A etapa de maximização (M), calcula parâmetros para maximizar a verossimilhança logarítmica encontrada na etapa E. Essas estimativas de parâmetro são usadas para determinar a distribuição das variáveis latentes na próxima etapa E, e o algoritmo se repete várias vezes (por isso é chamado iterativo).
Aplicações dessa ferramenta
Algoritmo de maximização de expectativa tem como umas principais aplicações em “Machine Learning” , Visão Computacional e modelagem estatística.
Tem alguns aplicações em “NLP”(Processsamento de Linguagem Natural).duas instâncias proeminentes do algoritmo são o algoritmo de Baum-Welch para modelos ocultos de Markov e o algoritmo de dentro para fora para indução não supervisionada de gramáticas livres de contexto estocásticas.
Tem alguns aplicações na área da saúde como a reconstrução de imagens médicas, especialmente em tomografia por emissão de pósitrons, tomografia computadorizada por emissão de fóton único, e tomografia computadorizada ,na área da psicometria, o EM é quase indispensável para estimar parâmetros de itens e habilidades latentes nos modelos de teoria de respostas ao item.O algoritmo de EM é usado para estimativa de parâmetros de modelos de misturas gaussianas,principalmente na genética quantitativa.
Na engenharia estrutural, o algoritmo de Identificação Estrutural usando Maximização de Expectativas (STRIDE, sigla do inglês) é um método somente de saída para identificar propriedades de vibração natural de um sistema estrutural usando dados de sensores (consulte Análise Modal Operacional).
A seguir iremos motrar um pouco dessa ferramenta com aplicações em dados por meio do program R e essa ferramenta está presente em alguns pacotes como
MCluster,
frailtyEM,
turboEM,
etc.
É importante saber algumas etapas e alguns conceitos que é nescessário para a aplicação.
Como funciona o Algoritmo EM ?
Dado um modelo estatístico que gera um conjunto
Com isso cria-se um modelo
Etapa de expectativa : os dados (ausentes) são estimados dado os dados observados e as estimativas atuais dos parâmetros do modelo calcula-se o valor esperado da função de probabilidade de
Etapa de maximização: A função de probabilidade é maximizada sob a suposição de que os dados (ausentes) são conhecidos com isso essa etapa encontra o parâmetro que maximiza essa quantidade.
No R
Função no R para calcular a etapa E e M do algoritimo , lembrando que é nescessário a normalidade dos dados !!!!!
Nesse caso vamos usar o pacote mvtnorm para ter um distribuição Multivariada da Normal.
#
#O código a seguir é baseado em algoritmos observados em
# Murphy,2012 Probabilistic Machine Learning,
# especificamente, Capítulo 11, seção 4.
#
em_mixture <- function(
params,
X,
clusters = 2,
tol = .00001,
maxits = 100,
showits = TRUE
) {
require(mvtnorm , quietly = TRUE)
N = nrow(X)
mu = params$mu
var = params$var
probs = params$probs
ri = matrix(0, ncol=clusters, nrow=N)
ll = 0
it = 0
converged = FALSE
if (showits)
cat(paste("Interações do EM:", "\n"))
while (!converged & it < maxits) {
probsOld = probs
llOld = ll
riOld = ri
### Parte E
for (k in 1:clusters){
ri[,k] = probs[k] * dmvnorm(X, mu[k, ], sigma = var[[k]], log = FALSE)
}
ri = ri/rowSums(ri)
### Parte M
rk = colSums(ri)
probs = rk/N
for (k in 1:clusters){
varmat = matrix(0, ncol = ncol(X), nrow = ncol(X))
for (i in 1:N){
varmat = varmat + ri[i,k] * X[i,]%*%t(X[i,])
}
mu[k,] = (t(X) %*% ri[,k]) / rk[k]
var[[k]] = varmat/rk[k] - mu[k,]%*%t(mu[k,])
ll[k] = -.5*sum( ri[,k] * dmvnorm(X, mu[k,], sigma = var[[k]], log = TRUE) )
}
ll = sum(ll)
parmlistold = c(llOld, probsOld)
parmlistcurrent = c(ll, probs)
it = it + 1
if (showits & it == 1 | it%%5 == 0)
cat(paste(format(it), "...", "\n", sep = ""))
converged = min(abs(parmlistold - parmlistcurrent)) <= tol
}
clust = which(round(ri) == 1, arr.ind = TRUE)
clust = clust[order(clust[,1]), 2]
list(
probs = probs,
mu = mu,
var = var,
resp = ri,
cluster = clust,
ll = ll
)
} Cluster com EM
Vamos Fazer agora um cluster com EM.
###
#
# Code by : Thalis Rebouças
#
###
# Library's Nescessarias para essa aplicação.
library(dplyr,quietly = TRUE)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionlibrary(purrr ,quietly = TRUE)
library(mclust, quietly = TRUE)## Package 'mclust' version 5.4.9
## Type 'citation("mclust")' for citing this R package in publications.##
## Attaching package: 'mclust'## The following object is masked from 'package:purrr':
##
## mapiris2 = iris %>%
dplyr::select(-Species) %>%
as.matrix()
mustart = iris %>%
dplyr::group_by(Species) %>%
dplyr::summarise(across(.fns = function(x) mean(x) + runif(1, 0, .5))) %>%
dplyr::select(-Species) %>%
as.matrix()
# usando purrr::map para fazer o mclust::map masking
covstart = iris %>%
split(.$Species) %>%
purrr::map(select, -Species) %>%
purrr::map(function(x) cov(x) + diag(runif(4, 0, .5)))
probs = c(.1, .2, .7)
starts = list(mu = mustart, var = covstart, probs = probs)
em_iris = em_mixture(
params = starts,
X = iris2,
clusters = 3,
tol = 1e-8,
maxits = 1500,
showits = T
)##
## Attaching package: 'mvtnorm'## The following object is masked from 'package:mclust':
##
## dmvnorm## Interações do EM:
## 1...# Verificando
table(em_iris$cluster, iris$Species)##
## setosa versicolor virginica
## 1 50 0 0
## 2 0 50 6
## 3 0 0 44Plotando o grafico sem as classes
library(ggplot2,quietly = TRUE)
library(plotly,quietly = TRUE)##
## Attaching package: 'plotly'## The following object is masked from 'package:ggplot2':
##
## last_plot## The following object is masked from 'package:stats':
##
## filter## The following object is masked from 'package:graphics':
##
## layoutggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length))+
geom_point() +
theme_minimal()
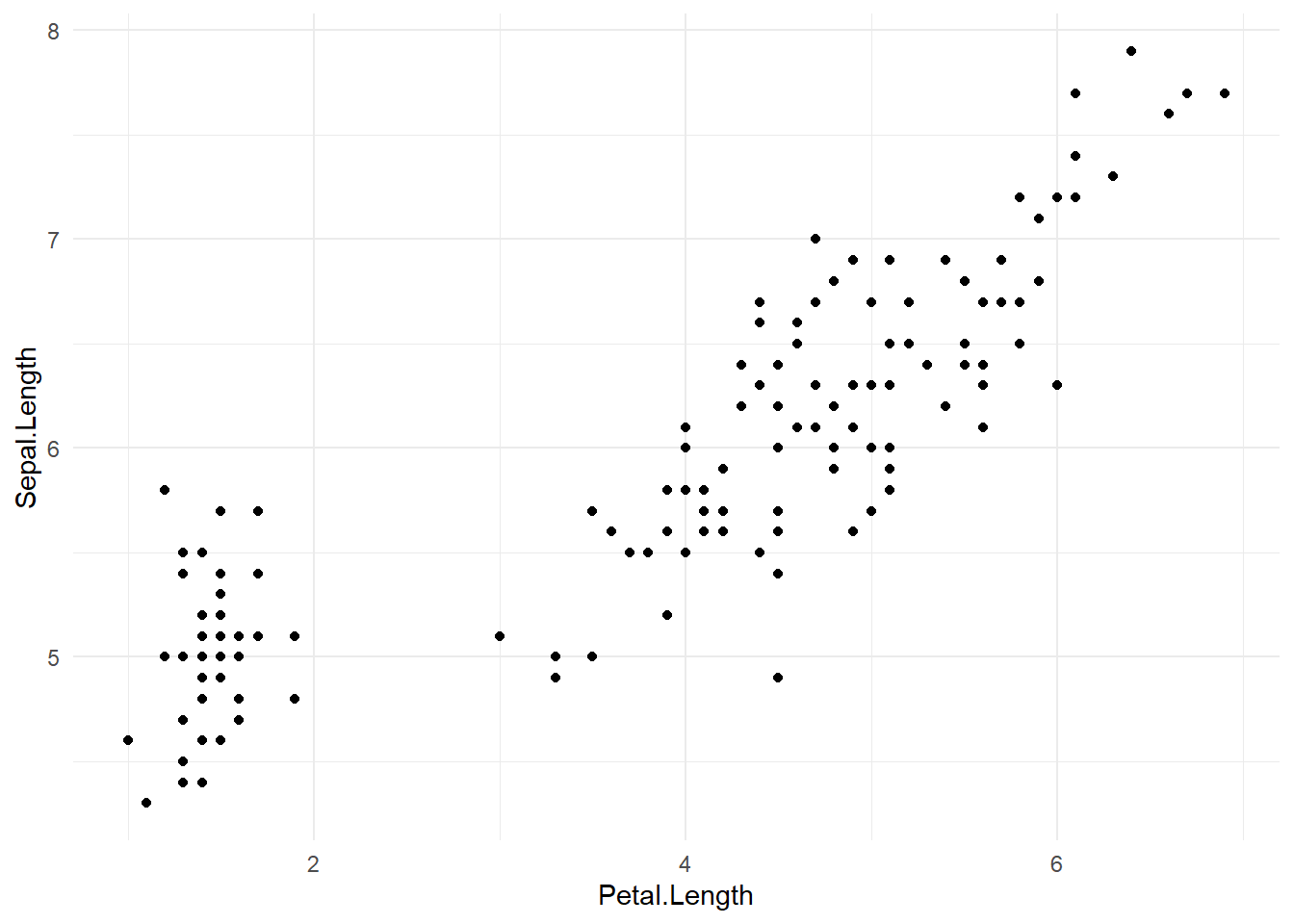
consegue identificar o padrão das espécies ?
Vamos ver os cluster’s
g1 <- ggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length))+
geom_point(aes(color = factor(em_iris$cluster)) , alpha = .7) +
geom_density2d(alpha = .2) +
scale_color_brewer(palette="Dark2") +
labs(colour = "cluster" , x = "Comprimento da Petala" , y= "Comprimento da Sepala")+
theme_minimal()
# Visualizando
plotly::ggplotly(g1)Qual a probilidade de uma especie está no cluster 2 ?
g2 <- ggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length)) +
geom_density2d(alpha = .2) +
geom_point(aes(color = em_iris$resp[, 2]) , alpha = .7)+
scale_color_gradient(low="blue", high="red") +
labs(colour = "Probabilidade de estar no cluster 2" , x = "Comprimento da Petala" , y= "Comprimento da Sepala")+
theme_minimal()
# visualizando
plotly::ggplotly(g2)Modo 2
mclust_iris = mclust::Mclust(iris[,1:4], 3)
table(mclust_iris$classification, iris$Species)##
## setosa versicolor virginica
## 1 50 0 0
## 2 0 45 0
## 3 0 5 50plot(mclust_iris, what = "density")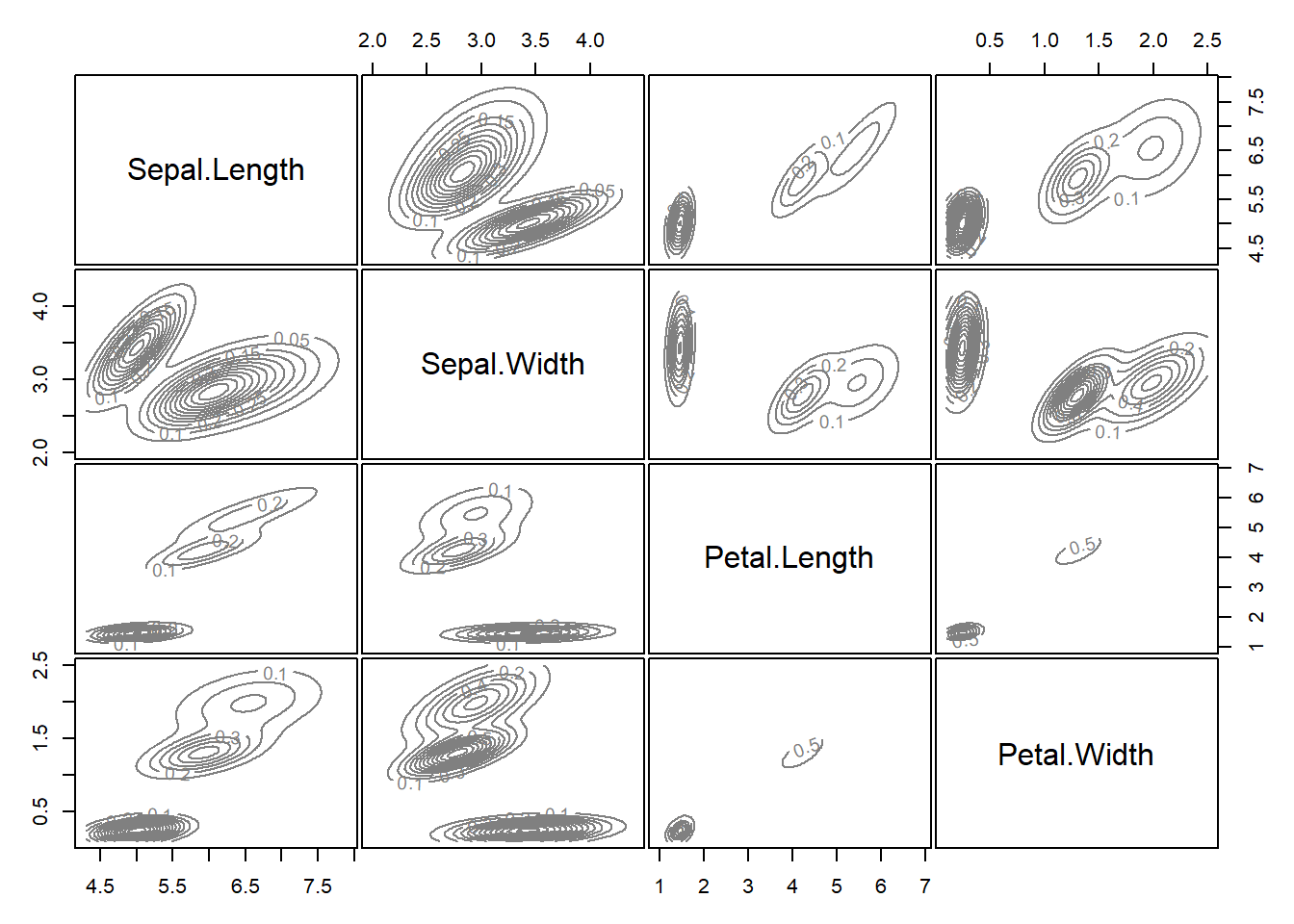
plot(mclust_iris, what=c("classification"), dimens=c(1,3)) 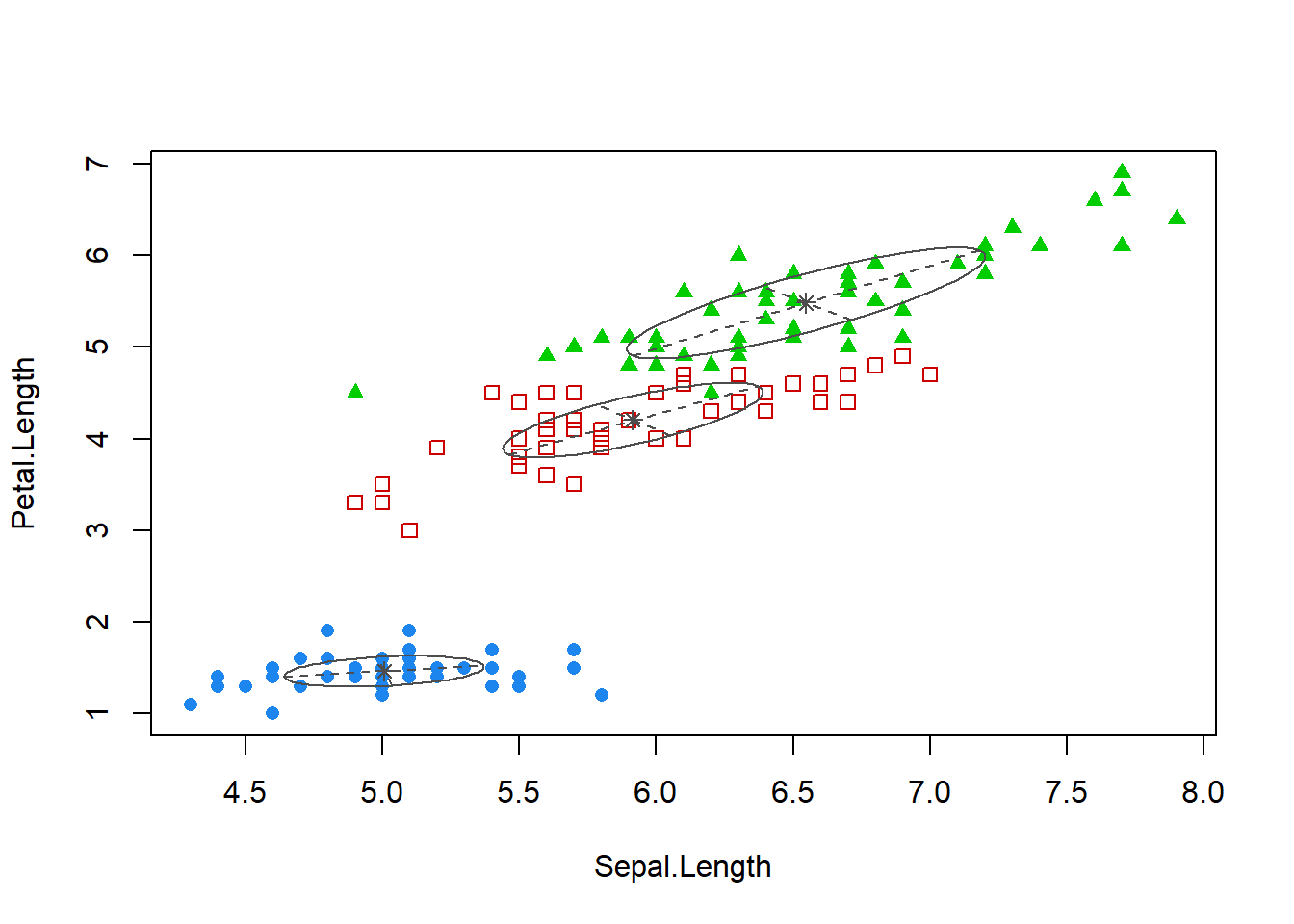
Algoritmo de maximização de expectativa
O que é ?
É um método interativo baseado em uma maximização para estimar os parâmentros da distribuições a partir dos dados da amostra. Os dados podem ser variáveis latentes, ou seja, não observadas de forma quantitativa inicialmente, nesta ferramentas pode utilizar o banco de dados com dados faltantes, pois em uma das etapas ocorre a imputação de dados para estimar o modelo.
A iteração EM alterna entre executar uma etapa de expectativa (E) e uma de maximização (M). A etapa de expectativa cria uma função para a expectativa da verossimilhança logarítmica usando a estimativa atual para os parâmetros. A etapa de maximização (M), calcula parâmetros para maximizar a verossimilhança logarítmica encontrada na etapa E. Essas estimativas de parâmetro são usadas para determinar a distribuição das variáveis latentes na próxima etapa E, e o algoritmo se repete várias vezes (por isso é chamado iterativo).
Aplicações dessa ferramenta
Algoritmo de maximização de expectativa tem como umas principais aplicações em “Machine Learning” , Visão Computacional e modelagem estatística.
Tem alguns aplicações em “NLP”(Processsamento de Linguagem Natural).duas instâncias proeminentes do algoritmo são o algoritmo de Baum-Welch para modelos ocultos de Markov e o algoritmo de dentro para fora para indução não supervisionada de gramáticas livres de contexto estocásticas.
Tem alguns aplicações na área da saúde como a reconstrução de imagens médicas, especialmente em tomografia por emissão de pósitrons, tomografia computadorizada por emissão de fóton único, e tomografia computadorizada ,na área da psicometria, o EM é quase indispensável para estimar parâmetros de itens e habilidades latentes nos modelos de teoria de respostas ao item.O algoritmo de EM é usado para estimativa de parâmetros de modelos de misturas gaussianas,principalmente na genética quantitativa.
Na engenharia estrutural, o algoritmo de Identificação Estrutural usando Maximização de Expectativas (STRIDE, sigla do inglês) é um método somente de saída para identificar propriedades de vibração natural de um sistema estrutural usando dados de sensores (consulte Análise Modal Operacional).
A seguir iremos motrar um pouco dessa ferramenta com aplicações em dados por meio do program R e essa ferramenta está presente em alguns pacotes como MCluster, frailtyEM, turboEM, etc. É importante saber algumas etapas e alguns conceitos que é nescessário para a aplicação.
Como funciona o Algoritmo EM ?
Dado um modelo estatístico que gera um conjunto
Com isso cria-se um modelo
Etapa de expectativa : os dados (ausentes) são estimados dado os dados observados e as estimativas atuais dos parâmetros do modelo calcula-se o valor esperado da função de probabilidade de
Etapa de maximização: A função de probabilidade é maximizada sob a suposição de que os dados (ausentes) são conhecidos com isso essa etapa encontra o parâmetro que maximiza essa quantidade.
No R
Função no R para calcular a etapa E e M do algoritimo , lembrando que é nescessário a normalidade dos dados !!!!!
Nesse caso vamos usar o pacote mvtnorm para ter um distribuição Multivariada da Normal.
#
#O código a seguir é baseado em algoritmos observados em
# Murphy,2012 Probabilistic Machine Learning,
# especificamente, Capítulo 11, seção 4.
#
em_mixture <- function(
params,
X,
clusters = 2,
tol = .00001,
maxits = 100,
showits = TRUE
) {
require(mvtnorm , quietly = TRUE)
N = nrow(X)
mu = params$mu
var = params$var
probs = params$probs
ri = matrix(0, ncol=clusters, nrow=N)
ll = 0
it = 0
converged = FALSE
if (showits)
cat(paste("Interações do EM:", "\n"))
while (!converged & it < maxits) {
probsOld = probs
llOld = ll
riOld = ri
### Parte E
for (k in 1:clusters){
ri[,k] = probs[k] * dmvnorm(X, mu[k, ], sigma = var[[k]], log = FALSE)
}
ri = ri/rowSums(ri)
### Parte M
rk = colSums(ri)
probs = rk/N
for (k in 1:clusters){
varmat = matrix(0, ncol = ncol(X), nrow = ncol(X))
for (i in 1:N){
varmat = varmat + ri[i,k] * X[i,]%*%t(X[i,])
}
mu[k,] = (t(X) %*% ri[,k]) / rk[k]
var[[k]] = varmat/rk[k] - mu[k,]%*%t(mu[k,])
ll[k] = -.5*sum( ri[,k] * dmvnorm(X, mu[k,], sigma = var[[k]], log = TRUE) )
}
ll = sum(ll)
parmlistold = c(llOld, probsOld)
parmlistcurrent = c(ll, probs)
it = it + 1
if (showits & it == 1 | it%%5 == 0)
cat(paste(format(it), "...", "\n", sep = ""))
converged = min(abs(parmlistold - parmlistcurrent)) <= tol
}
clust = which(round(ri) == 1, arr.ind = TRUE)
clust = clust[order(clust[,1]), 2]
list(
probs = probs,
mu = mu,
var = var,
resp = ri,
cluster = clust,
ll = ll
)
} Cluster com EM
Vamos Fazer agora um cluster com EM.
###
#
# Code by : Thalis Rebouças
#
###
# Library's Nescessarias para essa aplicação.
library(dplyr,quietly = TRUE)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionlibrary(purrr ,quietly = TRUE)
library(mclust, quietly = TRUE)## Package 'mclust' version 5.4.9
## Type 'citation("mclust")' for citing this R package in publications.##
## Attaching package: 'mclust'## The following object is masked from 'package:purrr':
##
## mapiris2 = iris %>%
dplyr::select(-Species) %>%
as.matrix()
mustart = iris %>%
dplyr::group_by(Species) %>%
dplyr::summarise(across(.fns = function(x) mean(x) + runif(1, 0, .5))) %>%
dplyr::select(-Species) %>%
as.matrix()
# usando purrr::map para fazer o mclust::map masking
covstart = iris %>%
split(.$Species) %>%
purrr::map(select, -Species) %>%
purrr::map(function(x) cov(x) + diag(runif(4, 0, .5)))
probs = c(.1, .2, .7)
starts = list(mu = mustart, var = covstart, probs = probs)
em_iris = em_mixture(
params = starts,
X = iris2,
clusters = 3,
tol = 1e-8,
maxits = 1500,
showits = T
)##
## Attaching package: 'mvtnorm'## The following object is masked from 'package:mclust':
##
## dmvnorm## Interações do EM:
## 1...# Verificando
table(em_iris$cluster, iris$Species)##
## setosa versicolor virginica
## 1 50 0 0
## 2 0 50 6
## 3 0 0 44Plotando o grafico sem as classes
library(ggplot2,quietly = TRUE)
library(plotly,quietly = TRUE)##
## Attaching package: 'plotly'## The following object is masked from 'package:ggplot2':
##
## last_plot## The following object is masked from 'package:stats':
##
## filter## The following object is masked from 'package:graphics':
##
## layoutggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length))+
geom_point() +
theme_minimal()
consegue identificar o padrão das espécies ?
Vamos ver os cluster’s
g1 <- ggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length))+
geom_point(aes(color = factor(em_iris$cluster)) , alpha = .7) +
geom_density2d(alpha = .2) +
scale_color_brewer(palette="Dark2") +
labs(colour = "cluster" , x = "Comprimento da Petala" , y= "Comprimento da Sepala")+
theme_minimal()
# Visualizando
plotly::ggplotly(g1)Qual a probilidade de uma especie está no cluster 2 ?
g2 <- ggplot2::ggplot(data = iris,aes(x = Petal.Length, y = Sepal.Length)) +
geom_density2d(alpha = .2) +
geom_point(aes(color = em_iris$resp[, 2]) , alpha = .7)+
scale_color_gradient(low="blue", high="red") +
labs(colour = "Probabilidade de estar no cluster 2" , x = "Comprimento da Petala" , y= "Comprimento da Sepala")+
theme_minimal()
# visualizando
plotly::ggplotly(g2)Modo 2
mclust_iris = mclust::Mclust(iris[,1:4], 3)
table(mclust_iris$classification, iris$Species)##
## setosa versicolor virginica
## 1 50 0 0
## 2 0 45 0
## 3 0 5 50plot(mclust_iris, what = "density")
plot(mclust_iris, what=c("classification"), dimens=c(1,3)) 
- Anterior - Página 1
- Página 2
- Próxima - Página 2






