Regressão linear
Regressão Linear
O que é isso ?
A regressão é de maneira geral no caso simples é uma formula que você consegue gerar uma reta e essa reta descreve o comportamento de uma relação linear nos parâmetros e assim , conseguir entender o \(\alpha\) e o \(\beta\) que gera a reta assim conseguindo prever os possiveis valores ou (depende de normalidade essa parte) fazer inferência de segunda ordem.
Já na multipla não temos mais uma reta e sim um Hiperplano ,pronto finalizamos o resumo conceito, bora para as formulas :
Importante para fazer Regressão :
Linear Simples :
A coisa mais importante para fazer regressão são seus presupostos neste caso são cinco :
- A função de Regressão é Linear nos parâmtros.(\(\alpha\) e \(\beta\))
- Os valores dos \(x_i\) são fixos e conhecidos ,não são uma variável aleatória.
- Os erros tem média 0, ou seja, \(E[e_i|x_i] = 0\)
- Os erros tem varância 1 e constante (Homoscesdaticidade), ou seja, \(Var[e_i|x_i] = \sigma^2\)
- Os erros são não correlacionados, \(Cov(e_i,e_j) = E[e_ie_j]=0\)
A formula é dado por :
\[y_i = \alpha + \beta x_i + e_i\ \ i =1,...,n
\]
Linear Multipla :
- A função de Regressão é Linear nos parâmtros.(\(\alpha\) e \(\beta_n\))
- Os valores dos \(x_i\) são fixos e conhecidos, a matriz de especificação $X(n p) $ sendo não aleatória e de posto completo.
- Os erros tem média 0, ou seja, \(E[e_i|x_i] = 0\)
- Os erros tem varância 1 e constante (Homoscesdaticidade), ou seja, \(Var[e_i|x_i] = \sigma^2I_n\)
- Os erros são não correlacionados, \(Cov(e_i,e_j) = E[e_ie_j]=0\)
\[y_i = \alpha + \beta_1 x_{1i} +\beta_2 x_{2i} + e_i\ \ i =1,...,n
\]
Métodos dos Mínimos Quadrados:
Esse é o método padrão que o software R usa e com isso ele estima a melhor retá que minimiza a distância do valor observado para o valor ajustado da reta.
Estimação dos Parâmentros:
Neste caso o \(\alpha\) estimado da reta é dada pela seguinte formula :
\[\alpha = \bar{y}-\beta \bar{x}
\]
Onde o \(\bar{y}\) é a média amostral de \(Y\) ,que é a variável resposta e \(\bar{x}\) é a média dos \(x_i\),que são as variáveis explicativas.
Agora para estimar o \(\beta\) temos a seguinte formula :
\[\beta = \dfrac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2} = \dfrac{Sxy}{Sxx}
\]
Na forma matricial o \(\beta\) é dado pela seguinte formula :
\[\beta = (X^TX)^{-1}X^Ty
\]
Todas as provas deste metodo é disponibilizado neste site statproofbook na seção 1.4 e na seçãp 1.5 tem a provas em matrizes na forma multipla.O Teorema Gauss-Markov garante (embora indiretamente) que o estimador de mínimos quadrados é o estimador não-enviesado de mínima variância linear na variável resposta,caso siga uma distribuição normal.
Formula exata dos Parâmetros:
Uma das coisas importantes da estatística é saber a sua média e também a sua variânça,por isso, temos que :
Variância do \(\alpha\) :
\[Var[\hat{\alpha}] =\sigma^2(\frac{1}{n}+\frac{\bar{x}_n^2}{Sxx})
\]
Variância do \(\beta\) :
\[Var[\hat{\beta}] = \dfrac{\sigma^2}{Sxx}
\]
Covariância
\[Cov(\hat{\alpha},\hat{\beta})= -\dfrac{\sigma^2\hat{x}_n}{Sxx}\]
Os valores das variâncias são quantidades pivotais, ou seja, caso siga normalidade,podemos fazer intervalo de confiança e teste de hiposteses.
teste modo temos que a formula exata,seguindo normalidade, é dada por :
\[\hat{\alpha} \sim N(\alpha,\sigma^2(\frac{1}{n}+\frac{\bar{x}_n^2}{Sxx}))
\]
\[\hat{\beta} \sim N(\beta,\dfrac{\sigma^2}{Sxx})
\]
Resíduos:
Os resíduos são a diferença do valor observado menos o valor predito ,assim :
\[e_i = y_i-\hat{y_i}
\]
e temos que os resíduos segue um ruído branco :
\[e \sim RB(0,\sigma^2)
\]
O estimador para os resíduos é dado por :
\[\hat{e_i} = y_i - \hat{y_i} \sim (0 , 1 - \frac{1}{n}-\frac{(x_i-\bar{x_n})^2}{Sxx})
\]
ANOVA:
Temos a tabela da ANOVA, que possui os seguintes indicadores : Graus de Liberdade,Soma dos quadrados , Quadros médios e o Valor F(existência ou não de regressão)
Nela é possivel todos esses indicadores da Regressão,Resíduos e os totais .
Causa da Variação
GL
SQ
QM
F
Regressão
1
\(\sum_{i=1}^n(\hat{y}-\bar{y}_n)^2\)
Formula do lado dividido por 1
É a divisão do QMReg/QMRES
Resíduos
n-2
\(\sum_{i=1}^n(y-\hat{y}_n)^2\)
Formula do lado dividido por n - 2
Total
n-1
\(\sum_{i=1}^n(y-\bar{y}_n)^2\)
Formula do lado dividido por n -1
Intervalo de Confiança e Intervalo de Predição :
Para fazer os Intervalo de Confiança ,eu preciso dos estimadores vistos a cima e os désvios padrões que vão ser a nossa quantidade pivotal.
Para fazer os Intervalo de Predição, eu preciso dos valores preditos e o désvio padrão do \(\alpha\) que vai ser a nossa quantidade pivotal.
Regressão no R :
Para fazer Regressão no R vamos precisar dos seguintes pacotes o easystats ,tidyverse,tidymodels e plotly. A regressão é feita pelo comando lm(y~x) e no caso multiplo é só somar mais um variavel explicativa lm(y ~ x1+ x2).
Vamos pegar uma base como exemplo,usando a função report() do easystats para descrever a base de dados mtcars
# Pacote para abrir pacotes,atualizar e instalar os que não tem.
library(pacman)
# chamando os pacotes
pacman::p_load(easystats,tidyverse,tidymodels,tidygraph,plotly,car,kableExtra)
# base de dados mtcars
# Fazendo uma tabela com as principais medidas de posição e disperção.
report_table(mtcars) %>% select(-n_Missing) %>% kbl(digits = 2) %>%
kable_styling()
Variable
n_Obs
Mean
SD
Median
MAD
Min
Max
Skewness
Kurtosis
9
mpg
32
20.09
6.03
19.20
5.41
10.40
33.90
0.67
-0.02
7
cyl
32
6.19
1.79
6.00
2.97
4.00
8.00
-0.19
-1.76
11
disp
32
230.72
123.94
196.30
140.48
71.10
472.00
0.42
-1.07
10
hp
32
146.69
68.56
123.00
77.10
52.00
335.00
0.80
0.28
5
drat
32
3.60
0.53
3.70
0.70
2.76
4.93
0.29
-0.45
4
wt
32
3.22
0.98
3.33
0.77
1.51
5.42
0.47
0.42
8
qsec
32
17.85
1.79
17.71
1.42
14.50
22.90
0.41
0.86
2
vs
32
0.44
0.50
0.00
0.00
0.00
1.00
0.26
-2.06
1
am
32
0.41
0.50
0.00
0.00
0.00
1.00
0.40
-1.97
6
gear
32
3.69
0.74
4.00
1.48
3.00
5.00
0.58
-0.90
3
carb
32
2.81
1.62
2.00
1.48
1.00
8.00
1.16
2.02
# Vendo as correlações
plot(correlation(mtcars))+
scale_edge_color_continuous(low = "#000000", high = "#f55b14")
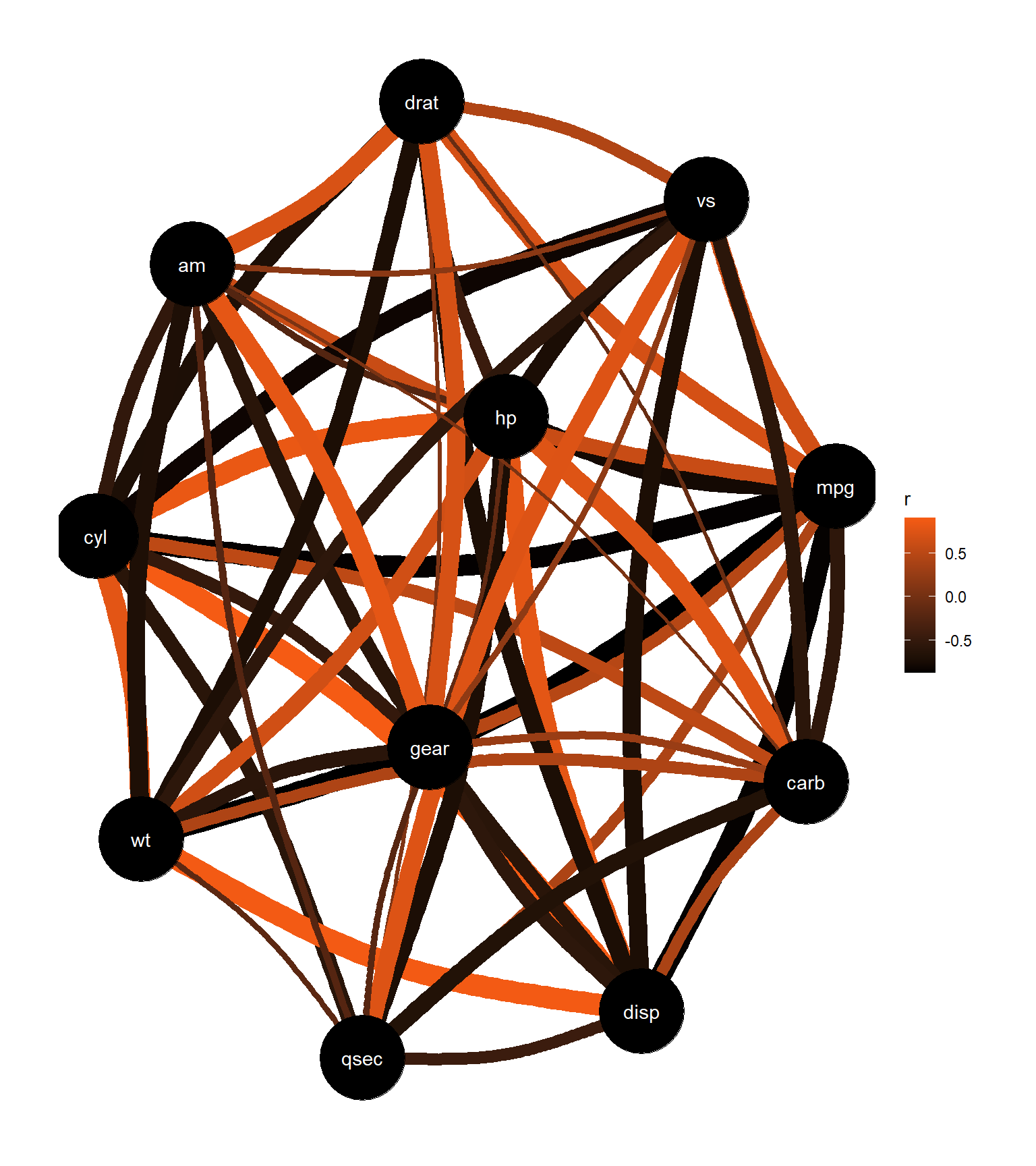
# Tabela de correlação
t1 <- correlation(mtcars)
# transformando em um tablea apresentavel
t1 %>%
dplyr::rename("p-value" = "p") %>%
dplyr::select(-CI,-df_error,-Method,-n_Obs,-t)%>% kbl(digits = 2) %>%
kable_styling()
Vamor ver agora se o “mpg” = Milhas por galão (do inglês Miles/(US) gallon) é explicador pelo número de cilíndros “cyl” , potêcnia “hp” e peso “wt”.
\[Mpg = b_0 + x_1b_1 + x_2b_2 + x_3b_3
\]
Para aplicar a relação de minimos quadrados no r é usado o comando ´lm()´.
modelo <- lm( mpg ~ cyl + hp +wt ,data = mtcars )
# checando o modelo
model_performance(modelo)
## # Indices of model performance
##
## AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
## -----------------------------------------------------
## 155.477 | 162.805 | 0.843 | 0.826 | 2.349 | 2.512
Temos que esse modelo consegue explicar cerca de 82,6% a consumo de combustivel dos carros pelo número de cilíndros ,potência e peso.
check_model(modelo)
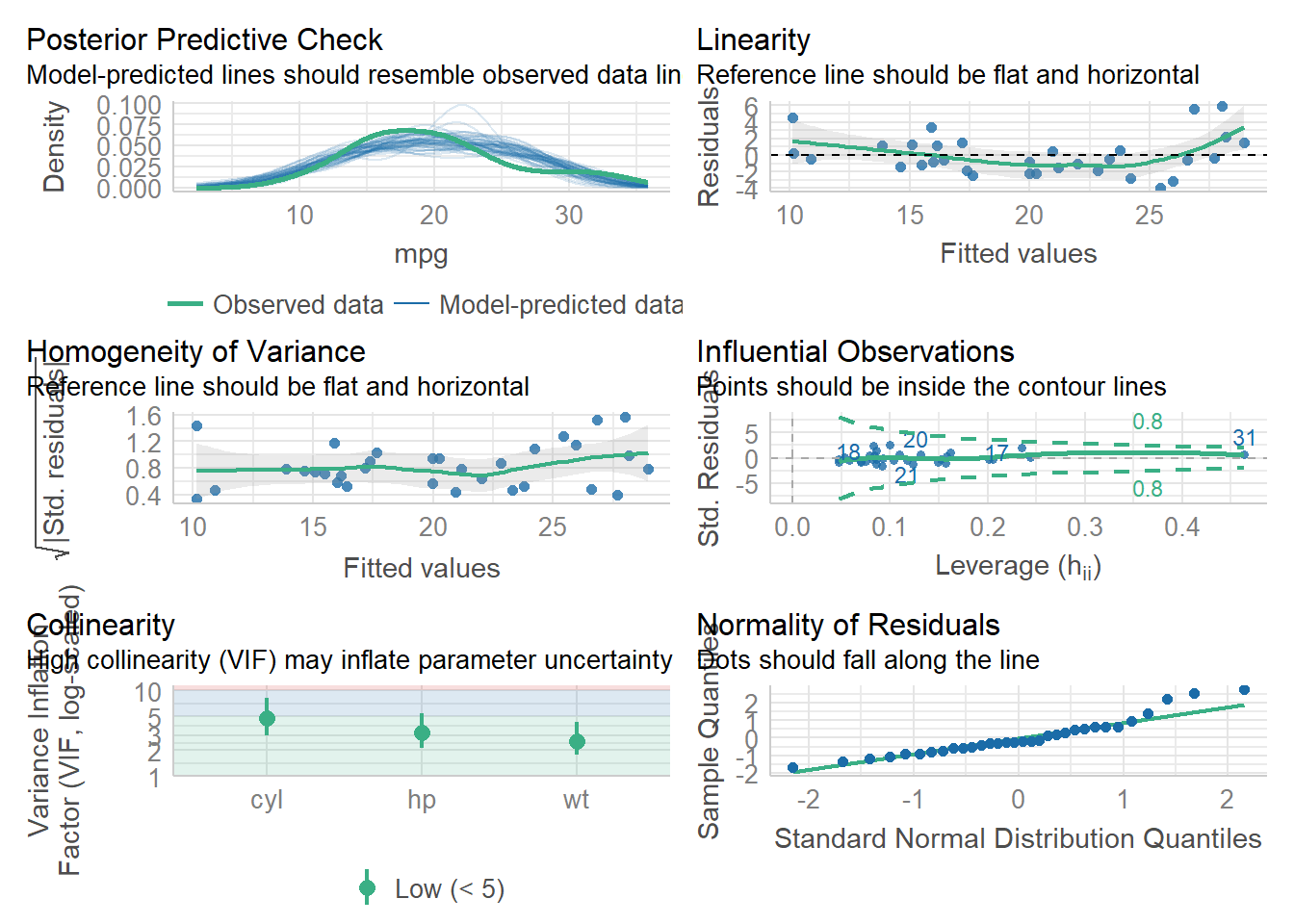Checando o modelo temos uma baixa colinearidade, ou seja, não temos variáveis explicando a mesma coisa, cada uma contribui de forma diferentes para ocorrer a regressão. Podemos dizer que a variância é homogênia,porém a temos que quanto mais consome combustivel os carros tem uma diferença possivelmente significativa. Temos alguns pontos influêntes ,porém não significativos.
O final temos o relátorio.
cat(report(modelo))
## We fitted a linear model (estimated using OLS) to predict mpg with cyl (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to cyl = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation. We fitted a linear model (estimated using OLS) to predict mpg with hp (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to hp = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation. We fitted a linear model (estimated using OLS) to predict mpg with wt (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to wt = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation.
Regressão Linear
O que é isso ?
A regressão é de maneira geral no caso simples é uma formula que você consegue gerar uma reta e essa reta descreve o comportamento de uma relação linear nos parâmetros e assim , conseguir entender o \(\alpha\) e o \(\beta\) que gera a reta assim conseguindo prever os possiveis valores ou (depende de normalidade essa parte) fazer inferência de segunda ordem.
Já na multipla não temos mais uma reta e sim um Hiperplano ,pronto finalizamos o resumo conceito, bora para as formulas :
Importante para fazer Regressão :
Linear Simples :
A coisa mais importante para fazer regressão são seus presupostos neste caso são cinco :
- A função de Regressão é Linear nos parâmtros.(\(\alpha\) e \(\beta\))
- Os valores dos \(x_i\) são fixos e conhecidos ,não são uma variável aleatória.
- Os erros tem média 0, ou seja, \(E[e_i|x_i] = 0\)
- Os erros tem varância 1 e constante (Homoscesdaticidade), ou seja, \(Var[e_i|x_i] = \sigma^2\)
- Os erros são não correlacionados, \(Cov(e_i,e_j) = E[e_ie_j]=0\)
A formula é dado por :
\[y_i = \alpha + \beta x_i + e_i\ \ i =1,...,n \]
Linear Multipla :
- A função de Regressão é Linear nos parâmtros.(\(\alpha\) e \(\beta_n\))
- Os valores dos \(x_i\) são fixos e conhecidos, a matriz de especificação $X(n p) $ sendo não aleatória e de posto completo.
- Os erros tem média 0, ou seja, \(E[e_i|x_i] = 0\)
- Os erros tem varância 1 e constante (Homoscesdaticidade), ou seja, \(Var[e_i|x_i] = \sigma^2I_n\)
- Os erros são não correlacionados, \(Cov(e_i,e_j) = E[e_ie_j]=0\)
\[y_i = \alpha + \beta_1 x_{1i} +\beta_2 x_{2i} + e_i\ \ i =1,...,n \]
Métodos dos Mínimos Quadrados:
Esse é o método padrão que o software R usa e com isso ele estima a melhor retá que minimiza a distância do valor observado para o valor ajustado da reta.
Estimação dos Parâmentros:
Neste caso o \(\alpha\) estimado da reta é dada pela seguinte formula :
\[\alpha = \bar{y}-\beta \bar{x} \]
Onde o \(\bar{y}\) é a média amostral de \(Y\) ,que é a variável resposta e \(\bar{x}\) é a média dos \(x_i\),que são as variáveis explicativas.
Agora para estimar o \(\beta\) temos a seguinte formula :
\[\beta = \dfrac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2} = \dfrac{Sxy}{Sxx} \]
Na forma matricial o \(\beta\) é dado pela seguinte formula :
\[\beta = (X^TX)^{-1}X^Ty \]
Todas as provas deste metodo é disponibilizado neste site statproofbook na seção 1.4 e na seçãp 1.5 tem a provas em matrizes na forma multipla.O Teorema Gauss-Markov garante (embora indiretamente) que o estimador de mínimos quadrados é o estimador não-enviesado de mínima variância linear na variável resposta,caso siga uma distribuição normal.
Formula exata dos Parâmetros:
Uma das coisas importantes da estatística é saber a sua média e também a sua variânça,por isso, temos que :
Variância do \(\alpha\) : \[Var[\hat{\alpha}] =\sigma^2(\frac{1}{n}+\frac{\bar{x}_n^2}{Sxx}) \]
Variância do \(\beta\) : \[Var[\hat{\beta}] = \dfrac{\sigma^2}{Sxx} \]
Covariância \[Cov(\hat{\alpha},\hat{\beta})= -\dfrac{\sigma^2\hat{x}_n}{Sxx}\]
Os valores das variâncias são quantidades pivotais, ou seja, caso siga normalidade,podemos fazer intervalo de confiança e teste de hiposteses.
teste modo temos que a formula exata,seguindo normalidade, é dada por :
\[\hat{\alpha} \sim N(\alpha,\sigma^2(\frac{1}{n}+\frac{\bar{x}_n^2}{Sxx})) \] \[\hat{\beta} \sim N(\beta,\dfrac{\sigma^2}{Sxx}) \]
Resíduos:
Os resíduos são a diferença do valor observado menos o valor predito ,assim :
\[e_i = y_i-\hat{y_i} \]
e temos que os resíduos segue um ruído branco :
\[e \sim RB(0,\sigma^2) \]
O estimador para os resíduos é dado por :
\[\hat{e_i} = y_i - \hat{y_i} \sim (0 , 1 - \frac{1}{n}-\frac{(x_i-\bar{x_n})^2}{Sxx}) \]
ANOVA:
Temos a tabela da ANOVA, que possui os seguintes indicadores : Graus de Liberdade,Soma dos quadrados , Quadros médios e o Valor F(existência ou não de regressão)
Nela é possivel todos esses indicadores da Regressão,Resíduos e os totais .
| Causa da Variação | GL | SQ | QM | F |
|---|---|---|---|---|
| Regressão | 1 | \(\sum_{i=1}^n(\hat{y}-\bar{y}_n)^2\) | Formula do lado dividido por 1 | É a divisão do QMReg/QMRES |
| Resíduos | n-2 | \(\sum_{i=1}^n(y-\hat{y}_n)^2\) | Formula do lado dividido por n - 2 | |
| Total | n-1 | \(\sum_{i=1}^n(y-\bar{y}_n)^2\) | Formula do lado dividido por n -1 |
Intervalo de Confiança e Intervalo de Predição :
Para fazer os Intervalo de Confiança ,eu preciso dos estimadores vistos a cima e os désvios padrões que vão ser a nossa quantidade pivotal.
Para fazer os Intervalo de Predição, eu preciso dos valores preditos e o désvio padrão do \(\alpha\) que vai ser a nossa quantidade pivotal.
Regressão no R :
Para fazer Regressão no R vamos precisar dos seguintes pacotes o easystats ,tidyverse,tidymodels e plotly. A regressão é feita pelo comando lm(y~x) e no caso multiplo é só somar mais um variavel explicativa lm(y ~ x1+ x2).
Vamos pegar uma base como exemplo,usando a função report() do easystats para descrever a base de dados mtcars
# Pacote para abrir pacotes,atualizar e instalar os que não tem.
library(pacman)
# chamando os pacotes
pacman::p_load(easystats,tidyverse,tidymodels,tidygraph,plotly,car,kableExtra)
# base de dados mtcars
# Fazendo uma tabela com as principais medidas de posição e disperção.
report_table(mtcars) %>% select(-n_Missing) %>% kbl(digits = 2) %>%
kable_styling()| Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|---|---|---|
| 9 | mpg | 32 | 20.09 | 6.03 | 19.20 | 5.41 | 10.40 | 33.90 | 0.67 | -0.02 |
| 7 | cyl | 32 | 6.19 | 1.79 | 6.00 | 2.97 | 4.00 | 8.00 | -0.19 | -1.76 |
| 11 | disp | 32 | 230.72 | 123.94 | 196.30 | 140.48 | 71.10 | 472.00 | 0.42 | -1.07 |
| 10 | hp | 32 | 146.69 | 68.56 | 123.00 | 77.10 | 52.00 | 335.00 | 0.80 | 0.28 |
| 5 | drat | 32 | 3.60 | 0.53 | 3.70 | 0.70 | 2.76 | 4.93 | 0.29 | -0.45 |
| 4 | wt | 32 | 3.22 | 0.98 | 3.33 | 0.77 | 1.51 | 5.42 | 0.47 | 0.42 |
| 8 | qsec | 32 | 17.85 | 1.79 | 17.71 | 1.42 | 14.50 | 22.90 | 0.41 | 0.86 |
| 2 | vs | 32 | 0.44 | 0.50 | 0.00 | 0.00 | 0.00 | 1.00 | 0.26 | -2.06 |
| 1 | am | 32 | 0.41 | 0.50 | 0.00 | 0.00 | 0.00 | 1.00 | 0.40 | -1.97 |
| 6 | gear | 32 | 3.69 | 0.74 | 4.00 | 1.48 | 3.00 | 5.00 | 0.58 | -0.90 |
| 3 | carb | 32 | 2.81 | 1.62 | 2.00 | 1.48 | 1.00 | 8.00 | 1.16 | 2.02 |
# Vendo as correlações
plot(correlation(mtcars))+
scale_edge_color_continuous(low = "#000000", high = "#f55b14")
# Tabela de correlação
t1 <- correlation(mtcars)
# transformando em um tablea apresentavel
t1 %>%
dplyr::rename("p-value" = "p") %>%
dplyr::select(-CI,-df_error,-Method,-n_Obs,-t)%>% kbl(digits = 2) %>%
kable_styling()Vamor ver agora se o “mpg” = Milhas por galão (do inglês Miles/(US) gallon) é explicador pelo número de cilíndros “cyl” , potêcnia “hp” e peso “wt”.
\[Mpg = b_0 + x_1b_1 + x_2b_2 + x_3b_3 \]
Para aplicar a relação de minimos quadrados no r é usado o comando ´lm()´.
modelo <- lm( mpg ~ cyl + hp +wt ,data = mtcars )
# checando o modelo
model_performance(modelo)## # Indices of model performance
##
## AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
## -----------------------------------------------------
## 155.477 | 162.805 | 0.843 | 0.826 | 2.349 | 2.512Temos que esse modelo consegue explicar cerca de 82,6% a consumo de combustivel dos carros pelo número de cilíndros ,potência e peso.
check_model(modelo)
Checando o modelo temos uma baixa colinearidade, ou seja, não temos variáveis explicando a mesma coisa, cada uma contribui de forma diferentes para ocorrer a regressão. Podemos dizer que a variância é homogênia,porém a temos que quanto mais consome combustivel os carros tem uma diferença possivelmente significativa. Temos alguns pontos influêntes ,porém não significativos.
O final temos o relátorio.
cat(report(modelo))## We fitted a linear model (estimated using OLS) to predict mpg with cyl (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to cyl = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation. We fitted a linear model (estimated using OLS) to predict mpg with hp (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to hp = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation. We fitted a linear model (estimated using OLS) to predict mpg with wt (formula: mpg ~ cyl + hp + wt). The model explains a statistically significant and substantial proportion of variance (R2 = 0.84, F(3, 28) = 50.17, p < .001, adj. R2 = 0.83). The model's intercept, corresponding to wt = 0, is at 38.75 (95% CI [35.09, 42.41], t(28) = 21.69, p < .001). Within this model:
##
## - The effect of cyl is statistically non-significant and negative (beta = -0.94, 95% CI [-2.07, 0.19], t(28) = -1.71, p = 0.098; Std. beta = -0.28, 95% CI [-0.61, 0.06])
## - The effect of hp is statistically non-significant and negative (beta = -0.02, 95% CI [-0.04, 6.29e-03], t(28) = -1.52, p = 0.140; Std. beta = -0.21, 95% CI [-0.48, 0.07])
## - The effect of wt is statistically significant and negative (beta = -3.17, 95% CI [-4.68, -1.65], t(28) = -4.28, p < .001; Std. beta = -0.51, 95% CI [-0.76, -0.27])
##
## Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation.01.Sobre mim:
02.Outras Postagens
- Anterior - Página 1
- Página 2
- Próxima - Página 2